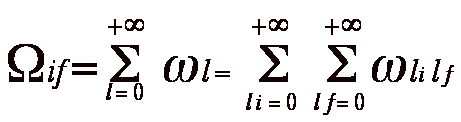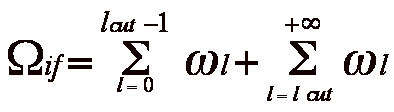RADIATIVE AND COLLISIONAL ATOMIC DATA FOR NEON-LIKE IONS
Marguerite Cornille and
Jacques Dubau
Observatoire de Paris
And
Sylvie Jacquemot
UMR7605 CNRS_CEA_Ecole Polytechnique_Universite ParisVI
Ecole Polytechnique 91128 Palaiseau cedex
Energy levels, radiative decay rates, and electron-impact collision strengths are presented for the following ions of the neon isoelectronic sequence: Fe XVII, Ge XXIII, Se XXV, Sr XXV, Mo XXXIII, and AG XXXVIII. Calculations are done for 65 levels that belong to the eight configurations 1s2 2s2 2p6, 1s2 2s2 2p5 3l (l = s, p, d), and 1s2 2s2 2p5 4l (l = s, p, d, f ). Well-know numerical codes were used for the atomic structure (SUPERSTRUCTURE) and electron-ion collision DISWAV/JAJOM) computations, toghether with an additional new code called JJOMCBE which calculates the contribution for high partial waves in the Coulomb-Bethe approximation ; relativistic effects were included in a fine-structure scheme. These atomic data are required for population kinetics modeling and spectral predictions in high-temperature plamas, especially for solar and x-ray laser applications.
Atomic Structure
The SUPERSTRUCTURE code developed at University College, London is well suited for computation of large quantities of atomic data for highly charged ions.
The wave functions are determined by diagonalization of the nonrelativistic Hamiltonian using orbitals calculated in a scaled Thomas-Fermi-Diarac-Amaldi potential. The scaling parameters ll (l =s, p, d), (lf=ld) have been obtained by a self-consistent energy minimization procedure, in our case on all 2p and 3l terms, and are listed in
TABLE A . Relativistic corrections are introduced according to the Breit-Pauli approach.
The calculated fine-structure energy levels corresponding to the large set of configurations defined above, that is 65 LSJ levels, are listed in
TABLE 1. A comparaison between the wavelentghs l we have computed and those from other theoretical works and from experiments is shown in
TABLE B for two selected Ne-like transitions :3s
1P
1 - 2p
1S
0 and 3p
3P
2 - 3s
1P
1 ; it can be seen that our calculations are very competitive for low and intermediate nuclear charge Z. The deviations observerd for higher Z values can be explained by the omission, in SUPERSTRUCTURE of QED and elaborate second-order effects, such as a
4 contribution, finite mass effect, and Fermi nuclear charge distribution of the nucleus.
In
TABLE 2 and
TABLE 3 are listed the dipole and quadrupole electric and magnetic(E1, E2, M1, M2) radiative transitions probabilities from our calculations. Ours results are in good agreemment with those published by others authors, as can be seen in
TABLE C.for the same two selected transitions as in
TABLE B.
We performed a complete (n = 2-3-4) set of calculations for the following atomic parameters : cross sections s, collision strengths W, and excitation rate coefficient Ce. These parameters are connected through simple equations as follows : for a given transition from the initial state i of the target-electron pair to its final state f, the cross section sif is given in terms of the collision strength Wif by
sif= Pa02Ec-1Ωifgi-1 (1)
where a
0 is the Bohr radius, E
c is the impact-electron energy (in rydberg) and g
i is the statistical weight of level i. If we assume a nonrelatisvistic Maxwellian distribution of the free electrons (characterized by an electron temperature T
E (in eV)), we obtain the excitation rate coefficient (in cm
3s
-1).
The DISWAV developped at University College, London treats the scattering of the electron (with a specified angular momentum l) by a Ne-like ion target (as defined by a set of eight configurations) in the distorted-wave approximation, to determine the nonrelativistic reactance matrix. The fine-structure collision strengths are provided by the code JAJOM through the transformation of the LS transition matrix elements into LSJ ones with the help of 'term-coupling coefficients' given by SUPERSTRUCTURE and of a 6-j Wigner coefficient subprogram. This method becomes very cumbersome for large l values, but since there may be a considerable contribution to Ωif from high partial waves, we cannot neglect them.
In the partial wave expansion, the collision strength Ωif can be expressed as a double summation over the orbital angular momenta li and lf of the projectile before (i) and after (f) the collision.
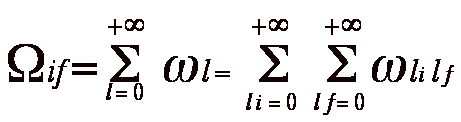
It is possible torewrite Eq. (2) as follows :
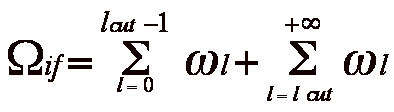
The first sum is directly calculated by the DISWAV/JAJOM package for l = 0 through l = 19 ( which corresponds to l
cut = 20).
For the optically allowed transitions the contribution from higher partial wave (here l > 19) is calculated by the JJOMCBE code and adapted by J. Dubau to be compatible with JAJOM.
Computations are done for all the transitions in the n= 2-3-4 for Se XXV at four incident elelectron energies (155, 200, 400, and 800 Ry) to follow the E
c dependendence of the collision strengths (
TABLE 4) and for the Fe, Ge, Sr, Mo, and Ag Ne-like ions (
TABLE 5) at one particular impact-electron energy, namely that corresponding to their respective upper 4f threshold at 85, 142, 214, 270, 355 RY.
In the present calculations, the convergence of the DISWAV/JAJOM and JJOMCBE approximations is checked carefully and essential perfect agreement if found when l = 19 (see
TABLE D
). The second sum is truncated for large l values to take into account plasma density effects. We have chosen the truncation cutoff at l = 50 for the allowed transitions listed in Table IV and Table V, which should ensure that virtualy all the collision strength values are well converged at all energies.
For the optically forbidden transitions the tabulated collision strengths include partial waves l = 0 trough 19 only. It has been shown that the infinite sum over the partial collision strengths is asymptotic to geometric series of ratio k
2f /k
2i where k
2i and k
2f are the energies of the colliding free electron before and after the collision. To check this asymptotic behavior, we have studied more precisely the 2p - 3p
transitions in SeXXV. The partial collision strengths for l = 14 through l = 19 have been calculated at two incident energies : 155 and 800 Ry. At lowest energy, the partial waves with l > 19 do not contribute to the collision strengths for any of the 2p - 3p transitions, while, at the highest energy, they contribute to the collision strengths only for thee transitions : 2p
1S
0- 3p
3D
2 ,
2p
1S
0 -3p
1D
2, and 2p
1S
0 - 3p
3P
2 (see
TABLE E ).
We have calculated the second term of Eq. (3) for lcut = 20 to l= 50. This contribution is not negligible, and thus the Ωif values in
TABLE 4 for these three collision strengths at 800 Ry may be underestimated by 15%. The collision strengths for the other 2p
1S
0 - n(n =3, 4 ; l = 0, 2, 3) forbidden transitions are less sensitive and are found to be underestimated by no more than 10% in SeXXV at 800 Ry.
The situation is less good for transitions between excited states. It can seen from
TABLE E that for some 3l - 3l' transitions (l = l' or l <> l') the l > 19 partial wave contribution at 800 Ry may be as much as 37%. For the 3l - 4l' transitions,
convergence is not good at 800 Ry. Collision stengths at 155Ry, on the other hand, are generally well converged for all transitions. An incident electron energy of 155 Ry is near the upper 4f threshold for Se XXV.
The collision strengths of the other ions are calculated for an incident electron
energy equal to the upper 4f threshold, for which the contribution of large angular momenta(l > 19) has been found to be small enough to be negligible.
A comparison (
TABLE F ) beween the n = 2 - 3 and n = 3 - 3 collision strengths obtained by us and those calculated by other authors is quite satisfactory. Unfortunately, no data for the n = 3 ' 4 and n = 4 ' 4 transitions are available for comparaison.